本記事はWantedly21新卒 Advent Calenderの16日目の記事です。

最近「効果検証入門 正しい比較のための因果推論/計量経済学の基礎」という本を読んでいます。学生時代に学んだ統計の知識を呼び起こしながら頑張って理解を進めています。また、業務上の施策でメールを送ることもあったので、その分析方法が正しかったのかを確認するためにも、ここでアウトプットすることにしました。今回のテーマは因果推論の基礎、セレクションバイアスです。

プロダクトの開発・運用において、ユーザーが何を求めているのかを知るのは最も重要なことです。しかし、ユーザーはそれを直接言ってくれません。直接聞いても答えてもらえるかわかりませんし、ユーザー自信でさえ何が本当に欲しいのかわからないかもしれません。私達はその答えを探し求め、効果的な施策を繰り返すことで、私達が作り出す世界観のもとユーザーの理想の状態に近づくことができます。そのためにも施策が効果的でなくてはなりません。

Wantedlyは「シゴトでココロオドルひとをふやす」ことを胸に日々プロダクトを進化させています。このことを踏まえると、私達にとって効果がある施策とはシゴトでココロオドルひとがふえる施策となります。例えばあなたがボスからメール施策を頼まれたとします。あなたは魅力的なメールを作成し、ユーザーに送信して、その効果をボスに報告しなくてはいけません。効果は「メール送信によってどれほどシゴトでココロオドルひとが増えたか」です(実際にはシゴトでココロオドルはyes/noのような2値ではないですが、ここでは2値として考えることとします)。

あなたは良い成果をボスに報告したいので、メール送信の対象者をより反応が良さそうな人たちに送りたいと考えました。そしてメール送信をした1週間でココロオドルひとがどれくらい増えたかをメールを送った人たちと送ってない人たちで比べます。ここでは比較する送信した人たちと送信してない人たちの数は同じと仮定し、結果が送信した人たちの中でココロオドルようになった人が5000人、送信しなかった人たちの中でココロオドルようになった人が2000人だったとします。単純に考えると3000人分の効果がメールにあったと思えてしまいます。しかし本当にあなたのメールは3000人もの人に効果を発揮したのでしょうか？

答えはNoです。これはメール対象者を選ぶ時点でバイアスが入ってしまっています。反応が良さそうな人達を選んでその人達の方がココロオドルようになるのは当たり前です。下の図を見てください。灰色の部分が何もしなくてもココロオドルようになる人の量を表しています。あなたが3000人分と言っていた効果は実際に反応が良さそうな人たちが自然にココロオドルようになる作用と実際のメールの効果を足したものになってしまっています。これは効果を過剰評価していることになってしまい、よく勘違いしてしまうポイントです。

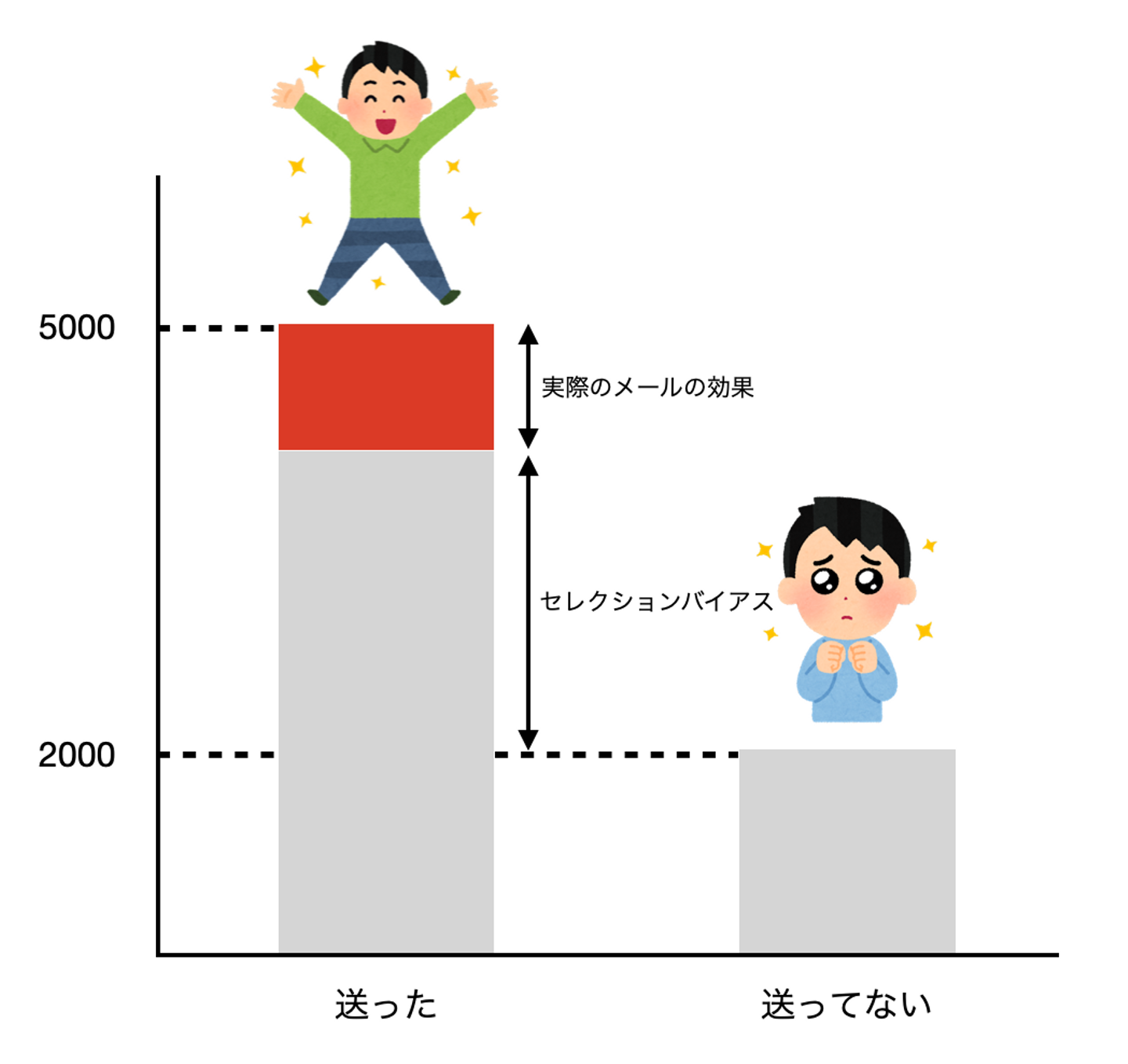
このようにメール対象者とそうでないユーザー間で何もしなかったときのココロオドルようになる人の量の部分をセレクションバイアスと呼びます。実際のメールの効果を述べたいときはこのセレクションバイアスが0のときの差を述べなくてはなりません。そうでないと、この勘違いが次の施策のスタンダードになり、また勘違いを生み出すという悪循環に陥ってしまいます。これはビジネス的にも避けたい状況の一つです。

セレクションバイアスをなくすために

先述のような間違いをしないために、セレクションバイアスを極力無くすことが重要です。最も完璧な方法は対象にメールを送った場合と送らなかった場合の両方観測することです。しかし、これは時間を戻せる力でも無い限り不可能な話です。そして実現可能な方法として、RCT(Randomized Control Trial)いわゆるABテストが存在します。RCTではメール対象を完全に無作為に選ぶことで、メールを受け取ったか受け取ってないか以外にユーザーの性質に差がない、つまりセレクションバイアスが無いということを仮定する方法です。メール送信対象のグループと送信しなかったグループはメール以外の平均的な要因は同じはずであり、平均の比較がそのままメールの効果そのものとなります。ここからは数式を用いてその意味を示していきましょう。

今、ユーザー i に対して、Zをメールを結果的に受け取ったかどうかとします。

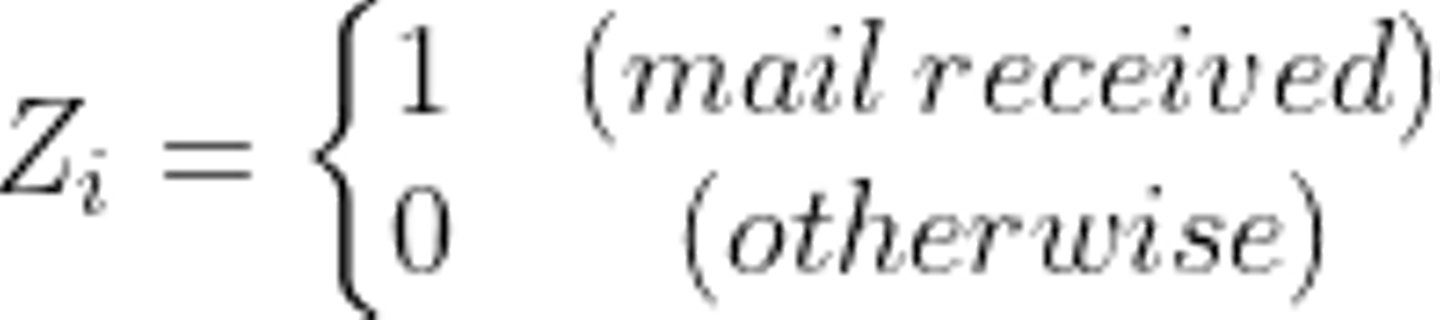
また、メールに限らずユーザー i がシゴトにココロオドルようになったかどうかを Yとおくことにします(必ず1か0の値をとります)。この値はメールを受け取ったかどうかで異なるので、それぞれZの値ごとに定義する必要があります。

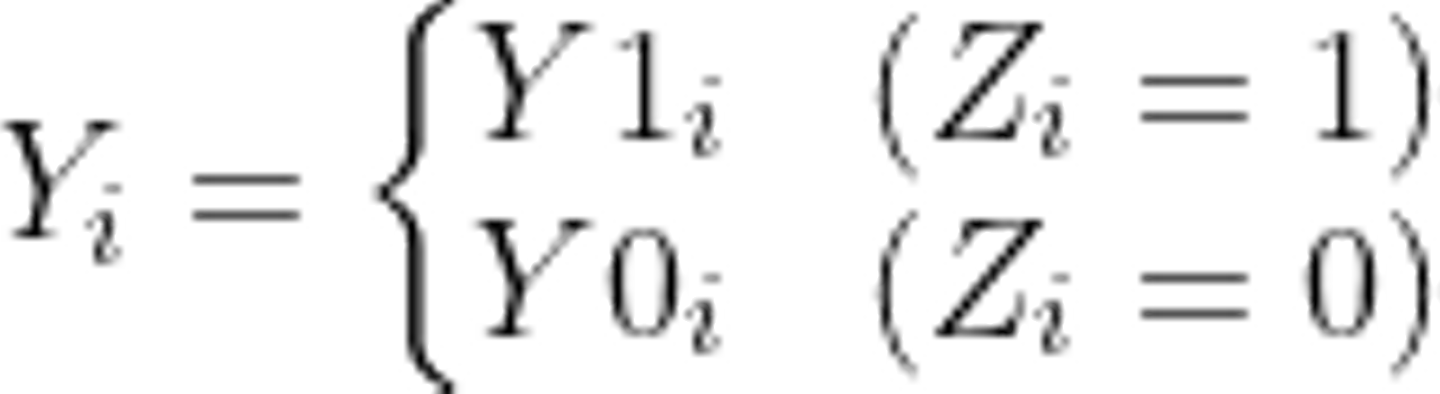
このとき、Zの値は1か0をどちらかを必ずとるので、一つの式にまとめてユーザー i の結果Yを以下のように表現できます。

ここまでの定義で、このユーザー i に対してメールの効果 τ は以下のように表せます。日本語で説明するとメールによってココロオドルようになったかどうかを意味しています。

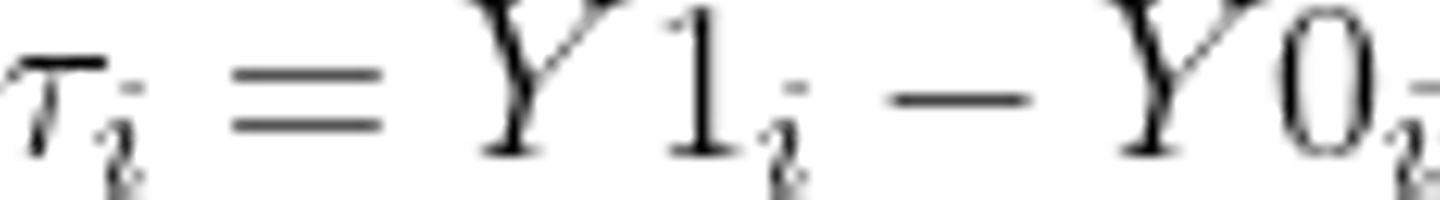
ただ、先程述べた通り同じ対象に対してメールを送った場合の結果とメールを送ってない場合の結果をどちらも観測することはできません。つまり、ユーザー i に対してY0かY1のどちらかしか観測できないのです。故にここからはユーザー１人１人に目を向けるのではなく、メールを送ったグループとそうでないグループの集団の平均的な振る舞いに目を向けることになります。先程のユーザー i におけるメールの効果を参考にグループにおける平均的なメールの効果として表すと以下のように示せます。

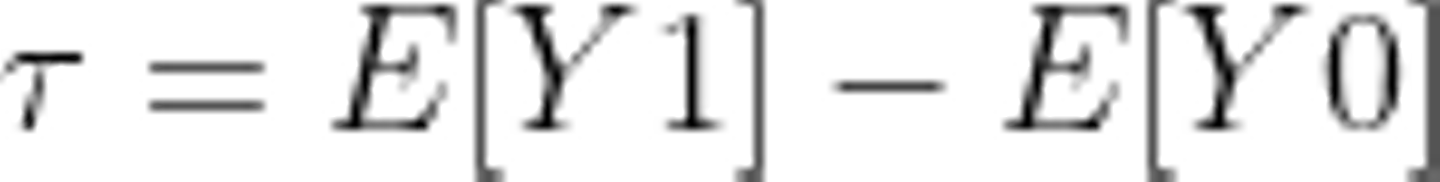
Eは期待値を表しています。これをユーザーごとに分解すると、結果YをZ=1のときと0のときの数で割った値、つまり平均を意味しています。ここで Nは今回の検証の対象ユーザーの全数となります。

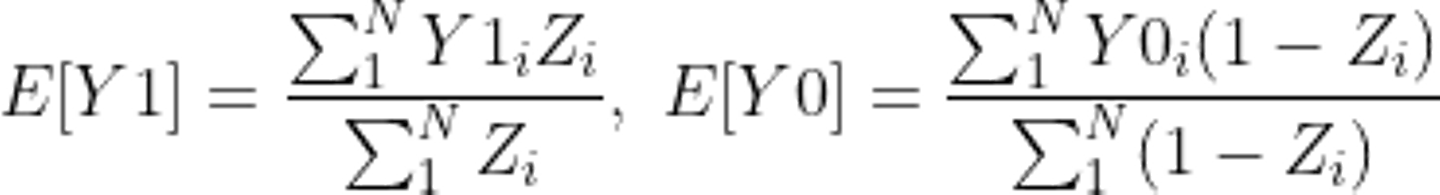
セレクションバイアスの正体

我々が今求めたいのはメールの効果τです。ここまで見るとそれぞれのグループの平均を計算して差分を求めているだけなので、3000人分の効果と言ってしまうのと同じ計算になってしまいます。どこか見落としが発生してそうです。重要なポイントとしては、今回は反応が良さそうなユーザーに意図的にメールを送ってしまったということです。つまり今回求めた平均は母集団の期待値 E[Y1] とは異なるということです。正確には、Z = 1 のときの条件付き期待値 E[Y1 | Z = 1] が今求めた平均が示していることです。今3000人の効果と言っているのは以下の式で表せます。ここでは間違ったメールの効果をτ'ということにします。

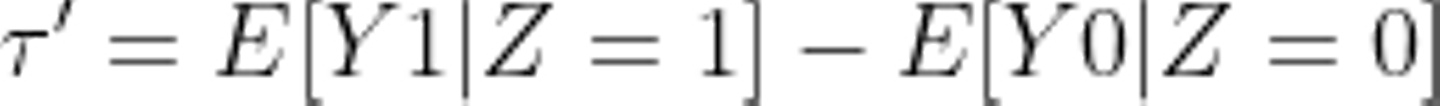
これを少し式変形して解像度を高めてみましょう。

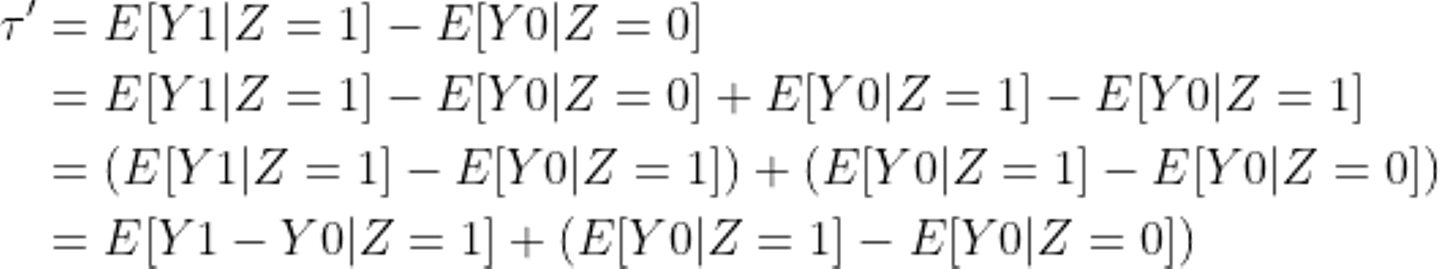
見た目は仰々しいですが、それほど難しいことはしていません。2行目ではただ単に E[Y0|Z=1] の正負を追加しています。3行目で式の順番を変えていて、4行目で条件Z=1のときでまとめているだけです。ここで、Zの値と効果の大きさに関係がないと仮定します。これはメールの送る送らないに関わらず効果があったときの値の大きさつまりシゴトでココロオドルかの2値間の大きさは関係無いことを仮定しています(もともと定義上1か0なので、効果があったら0から1となりこの差分は常に1である)。その仮定を式で表すと、

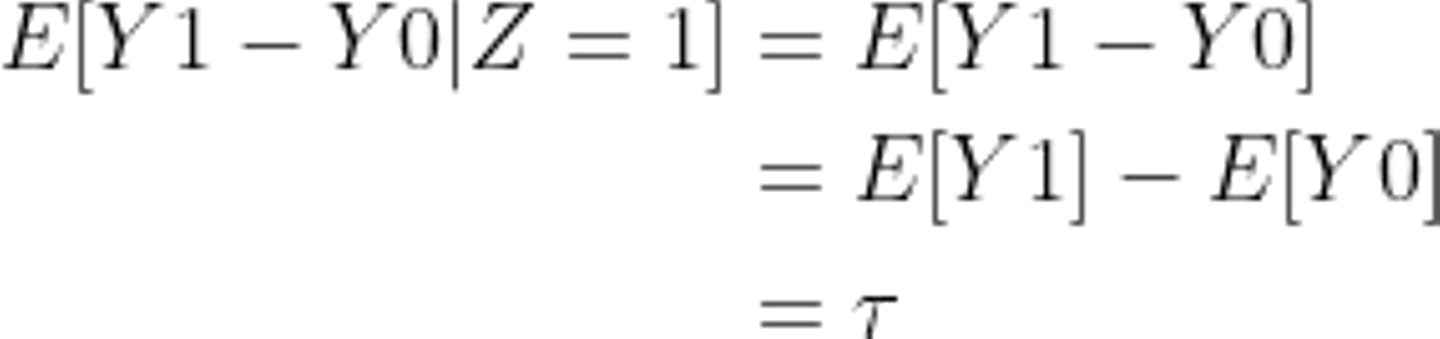
となります。これを先程の式に代入すると次のように表せます。

これがセレクションバイアスの正体です。E[Y0|Z=1] はメールを受け取ったグループがメールを受け取らなかったときの結果の期待値で、E[Y0|Z=0] はメールを受け取らなかったグループがメールを受け取らなかったときの結果の期待値です。もともと反応が良さそうなユーザーに送っていたのでこの差分は0以上になりそうですね。逆にこの差分が無いことを示せれば、グループごとの平均の差をそのままメールの効果と示すことができます。RCTでは完全にランダムにZを振り分けることによってセレクションバイアスを理論上0にして、検証することができます。

実際には有意差検定が必要

別の観点として、セレクションバイアスの式 E[Y0|Z=1] - E[Y0|Z=0] に検証対象の全数Nは依存していません。つまり、Nを大きくしたところで、バイアスが存在しなくなるということは無いのでそこを勘違いしてしまうと問題です。ここは分析の過程でよく間違われるポイントなので注意が必要です。

ただ、今回の検証では対象のN人は母集団からサイズNのサンプルを取り出していることに違いありません。つまり、N人でセレクションバイアスを取り除き効果があったとしても、実際の母集団では効果がないということがあります。そのためにはt検定に代表される有意差検定を行う必要があります。詳しくここでは述べませんが、このときにNの大きさによって信頼たる結果が得られているかどうかが関係してきます。Nを大きくした方がよいと言われるのはこちらの理由が主なのでしょう。この有意差検定でもセレクションバイアスが入っている場合、有意に差が出やすくなってしまうので、やはりセレクションバイアスを気にすることは重要になりそうです。

まとめ

今回は施策が本当に効果があるのかということを分析するために、メール施策を例にして注意すべき点を深ぼってみました。ある程度不確実性が多い中で、セレクションバイアスだけでなく多くの間違った仮定を置いてしまうことはビジネスにおいて生じてしまいます。今一度分析手法を見直して、間違った方向を向いてないか確認するのも手だと思います。なかなか難しいですがデータドリブンで進めていくためにもやっていき 💪 という感じですね！