CodeQUEEN2024で優勝しました

こんにちは、フォルシア株式会社エンジニアの宮本です。このたびCodeQUEEN2024というイベントに参加し、優勝することができました。この記事では当日のコンテストを振り返ります。

また、今年もフォルシアではCodeQUEENに協賛しスポンサー活動を実施しました。記事の最後ではスポンサーとして出題したクイズの解答も掲載したのでご覧ください。

昨年のブログ : https://www.forcia.com/blog/002760.html

CodeQUEENとは？

CodeQUEENは、AtCoder株式会社と合同会社AlgoParadeが共催する女性向けプログラミングコンテストです。コンテストの予選はオンライン、本選は全国の参加者が一堂に会して実施されます。

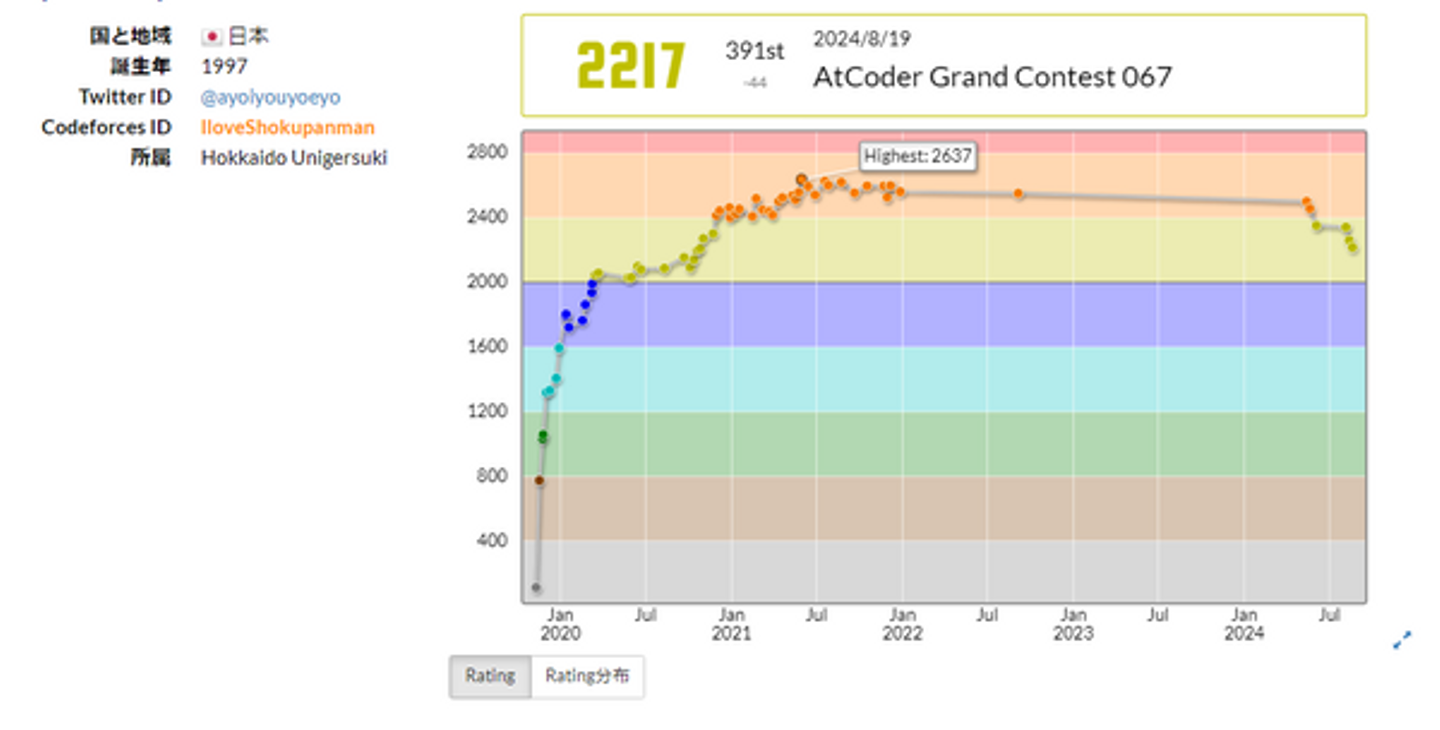
問題の形式はAtCoderと同じなので、競技プログラミングの力がいつも通り問われます。私は昨年度優勝することができ、今年は2連覇がかかっていました。しかし、ここ最近は競技プログラミングの成績が下降しており練習にもあまり時間が割けていなかったので、成績にはあまり期待せずコンテスト本選に参加しました。

競技プログラミングについて

競技プログラミングでは、与えられた入力に対して正しい答えを出力するプログラムを作成する問題が出題されます。『ゲームでどちらが勝つかを求める問題』『パズルの解法を求める問題』『ものの並べ方が何通りかを数える問題』など、色々な種類の問題があります。

競技プログラミングでは各問題に『実行時間制限』が与えられています。大抵の問題では全てのパターンを探索するプログラムを書いても実行時間制限に間に合いません。ちょうど、オセロの必勝法を求めるのに全パターン探索していたらいつまでも終わらないのと同じイメージです。問題を良く分析し実行時間に間に合うような効率的な解法を考えるのが競技プログラミングの面白さです。

以下の参加記では、競技プログラミングをやったことがない方にもなんとなくイメージが伝わればいいなと思い、一部の問題を図式化してみました。この記事を読んで興味を持ったら、ぜひ競技プログラミングに挑戦してみてください！

コンテスト本選の参加記

ネタバレを含むので、これから問題を解きたい方は読み飛ばしてください。

コンテストの本選では120分間で8問が出題されました。問題は後ろにいけばいくほど難易度があがり、その分配点が高くなります。最終的な得点の高い人が勝ち、同点の場合はタイムで順位が決まります。

CodeQUEENのような一発勝負のコンテストでは順位が大事なので必ずしもすべての問題を解こうとする必要はありません。現在の順位はリアルタイムで見ることができるので、まわりの様子をうかがいながら少しでも上の順位を目指します。

今回のコンテストでは後半に500点の問題が3問ありました。500点はCodeQUEEN参加者の上位層（青上位～黄色コーダー）で差がつく難易度なので、ここを何問拾えるかで優勝が決まると想定しました。一方、H問題の575点も全く手が届かない点数ではないので、他の参加者で解く人が現れると怖いなとも感じていました。

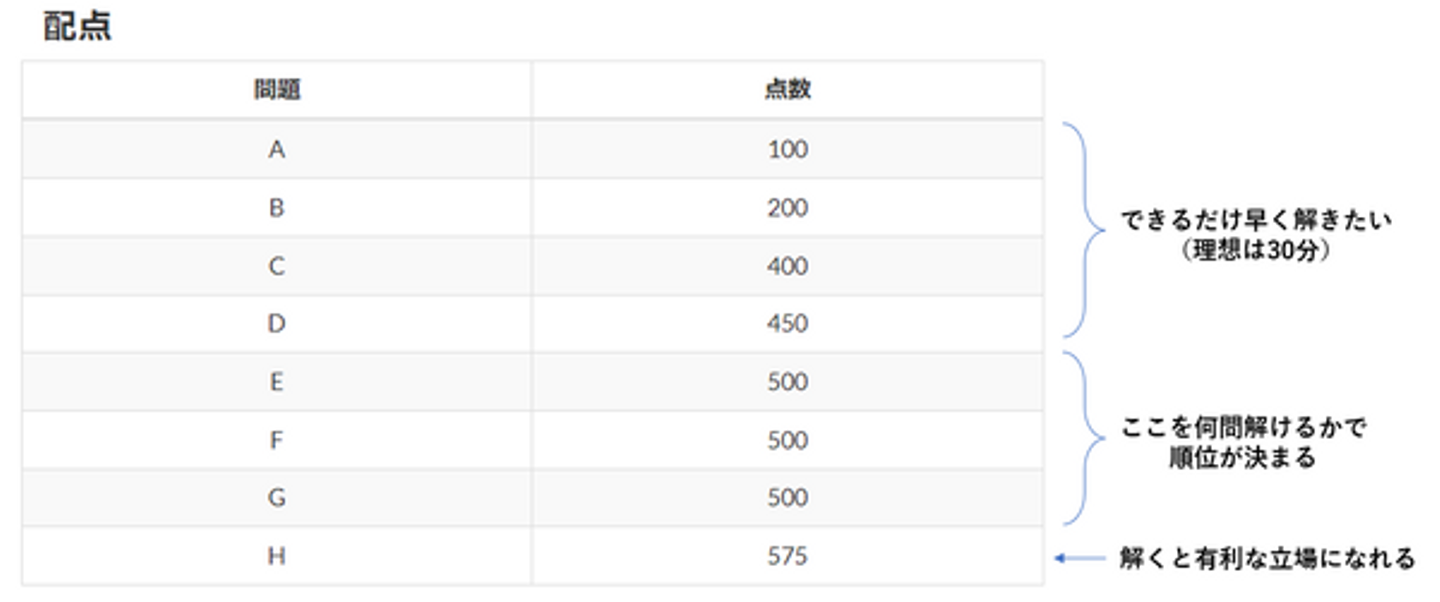
A問題～C問題

序盤は比較的簡単な問題が並びます。油断して不正解のコードを提出すると5分のタイムペナルティを受けるので、間違えないように確実に解き進めました。

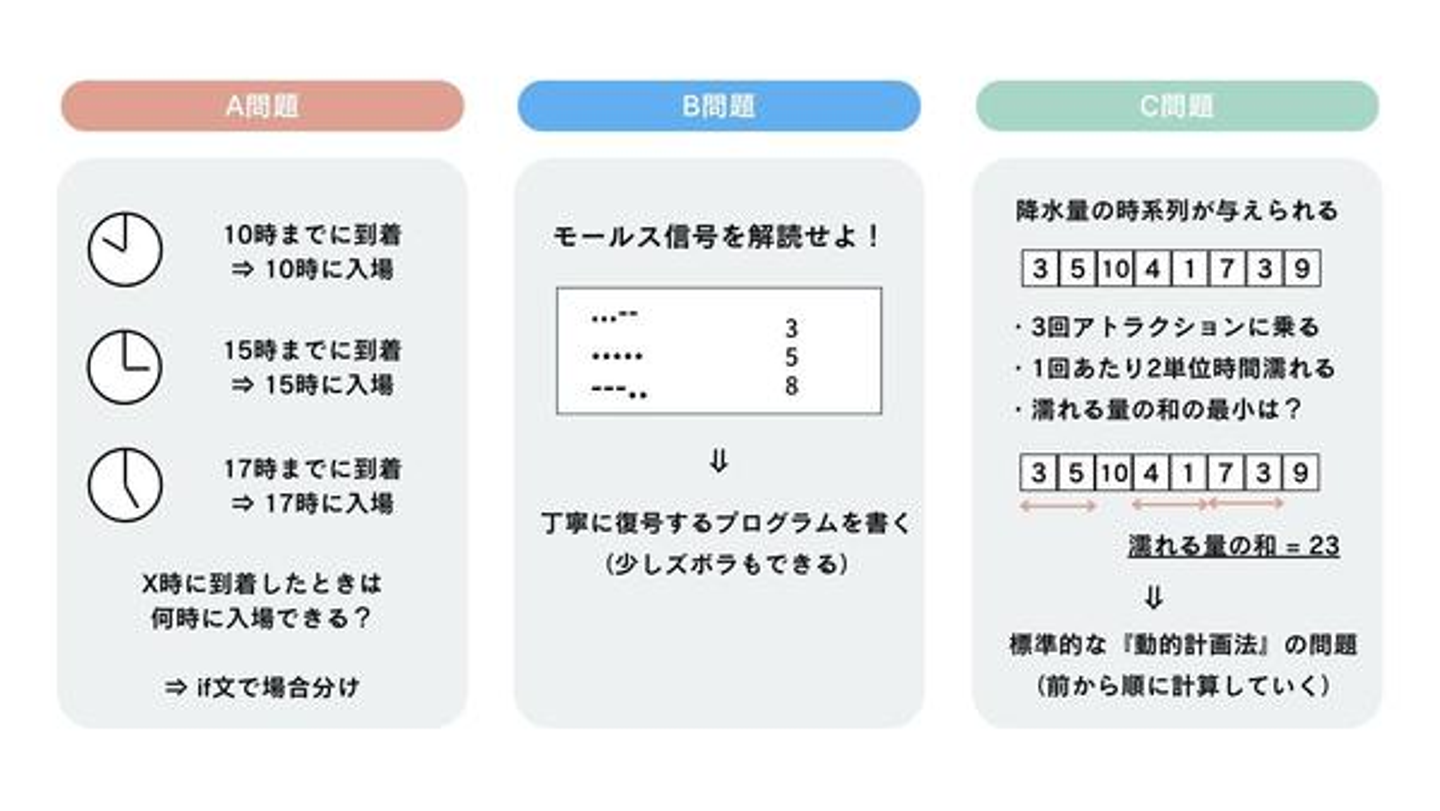
D問題 Attend Many Events

https://atcoder.jp/contests/codequeen2024-final-N9tn8QqD/tasks/codequeen2024_final_d

D問題では『ダイクストラ法』でグラフ上の2点間の最短距離を求めたあと、『動的計画法』で最適化問題を解きます。字面で書くと難しそうですが、いずれも競技プログラミングでは標準的なアルゴリズムです。また、問題の設定から解法の自由度はあまり高くない（＝初手で2点間の最短距離を求める以外にはやりようがない）ので、解法を考えるもの慣れていれば難しくありません。

私はダイクストラ法の実装方法を忘れて調べながら書いたので、この時点で他の参加者におくれをとってしまいました。

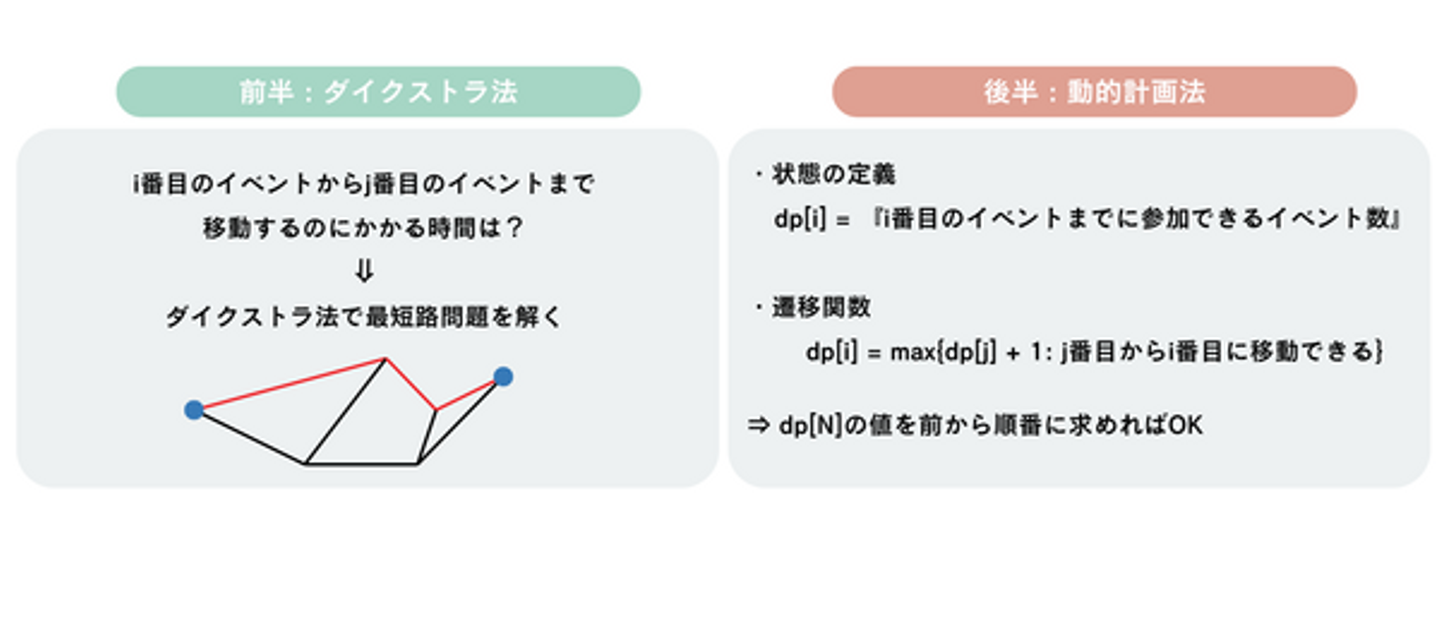
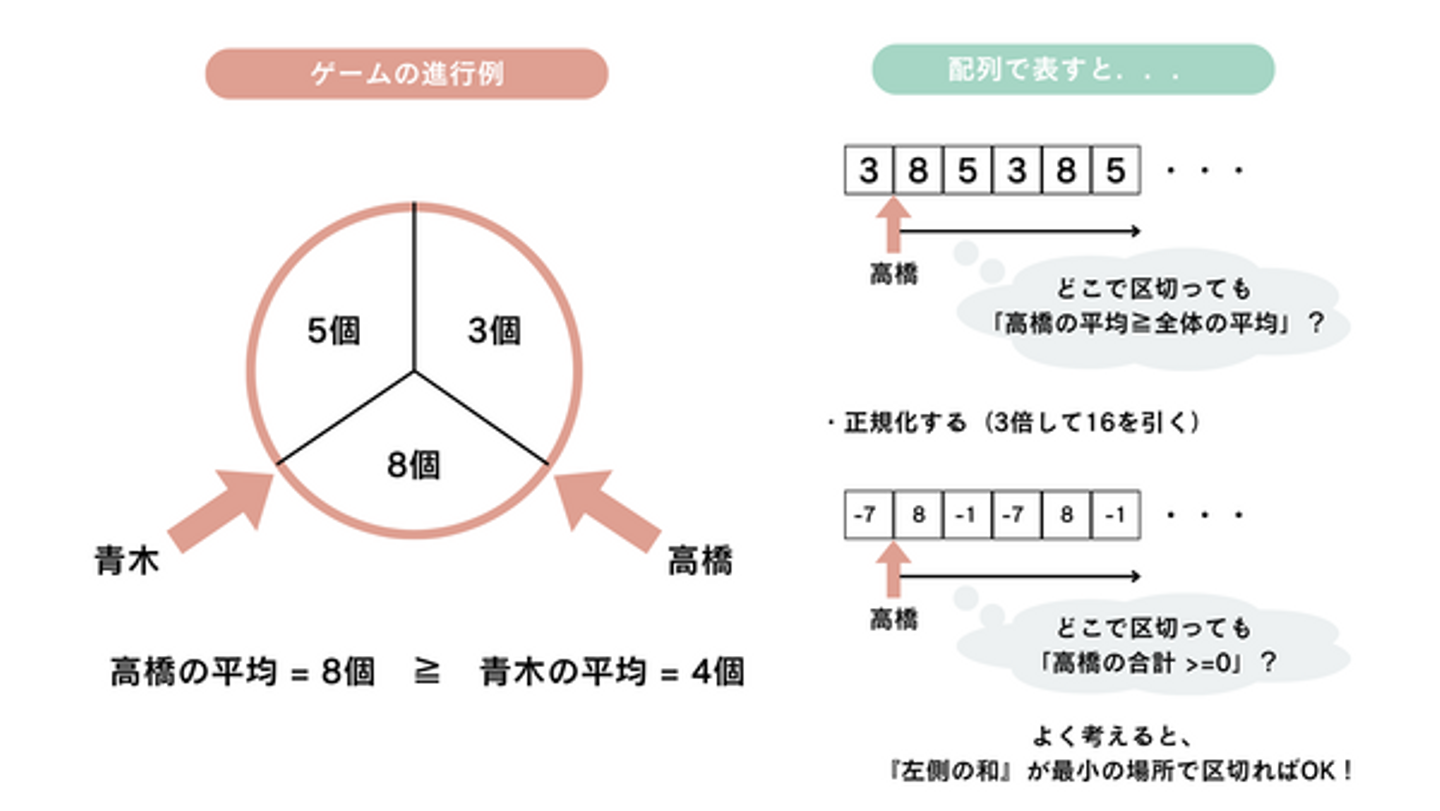
F問題 Divide the Cake

https://atcoder.jp/contests/codequeen2024-final-N9tn8QqD/tasks/codequeen2024_final_f

E問題は難しそうだったので、同じ得点のF問題を先に解くことにしました。いちごを取り合う対戦ゲームで勝つプレイヤーを答える問題でしたが、問題文をよく読むとゲーム自体にはほぼ戦略性がなく、配列処理のアルゴリズムを高速化することがメインです。この手の高速化はデータ構造を利用することが多く実装が複雑になりがちですが、今回は偶然良い方法を思いつきあっさりと解くことができました。

F問題を10分程度で正解できたことで優勝が大きく近づいたと感じます。

E問題 AtCoder Hotel

https://atcoder.jp/contests/codequeen2024-final-N9tn8QqD/tasks/codequeen2024_final_e

E問題はお客さんをホテルの部屋に割り当てていき、料金の和を最小化する問題です。それぞれのお客さんには「〇ランク以上の部屋に泊まりたい！」という要望があり、要望を満たすように部屋に割り当てていく必要があります。問題の雰囲気から最大流問題に帰着するかシンプルな動的計画法の問題かのいずれかと踏みましたが、順位表を見るとすでに解かれていたので動的計画法にヤマを張って考えました。

要望の厳しい客を高いランクの部屋から順に割り当てていく動的計画法を組み、20分程度で正解しました。