「なぜ野球では強打者が4番を打つのか?」
皆さんは考えたことがあるでしょうか。
単純に考えれば、「ランナーをためて4番に回した方がたくさん点を取れるからだ」と言うことができます。
果たして本当にそうでしょうか?
もし4番強打者論がデータに基づいて根付いた常識だとしたら、あまりにも昔から存在していると思いませんか?
実は強打者が3番や2番、もしかすると1番にいた方が得点を取れる確率が高いという可能性もあるのではないでしょうか。
今回はデータサイエンスの力を使って、最も得点を取りやすい打順を模索していきます!
目次
強打者が伝統的に4番に置かれる理由は?
データの力で最適な戦略を導く
検証~Pythonで実装してみる~
実装コード(Python)
①:クリーンナップ理論順
②:長打率順
③:打率順
結果の信頼性について
おわりに
強打者が伝統的に4番に置かれる理由は?
まずは、強打者が昔から4番に定着してきた理由を考えてみましょう。
それは、「クリーンナップ」の理論が存在するためです。
「1番・2番が出塁し、3~5番のクリーンナップで点を取る」という考え方に基づいています。
また、歴史や伝統による心理的な側面も大きいでしょう。
多くの人々の記憶に残る伝説の選手、ベーブ・ルースをはじめ、王貞治、長嶋茂雄、松井秀喜、落合博満、野村克也など多くのレジェンドが4番打者として活躍してきたことも、「4番=最強打者」というイメージを確たるものにしたと考えられます。
このような背景から、4番はそのチームの「顔」であり、最も長打力のある選手が置かれることが多いのです。
データの力で最適な戦略を導く
ここからはデータの力を使って、最適な戦略を見つけていきます。
今回はモンテカルロ法という確率的シミュレーション手法を使って、実験的に最適な戦略を求めていきます。
モンテカルロ法:
乱数を用いる無作為抽出により,問題の近似解を導く方法モンテカルロ法とは、「試行回数を増やすほど、試行によって計測された確率は真の確率の値に近づく」という統計学の法則を利用した手法です。
この法則を大数の法則と呼び、モンテカルロ法の有名な例としては円周率があります。
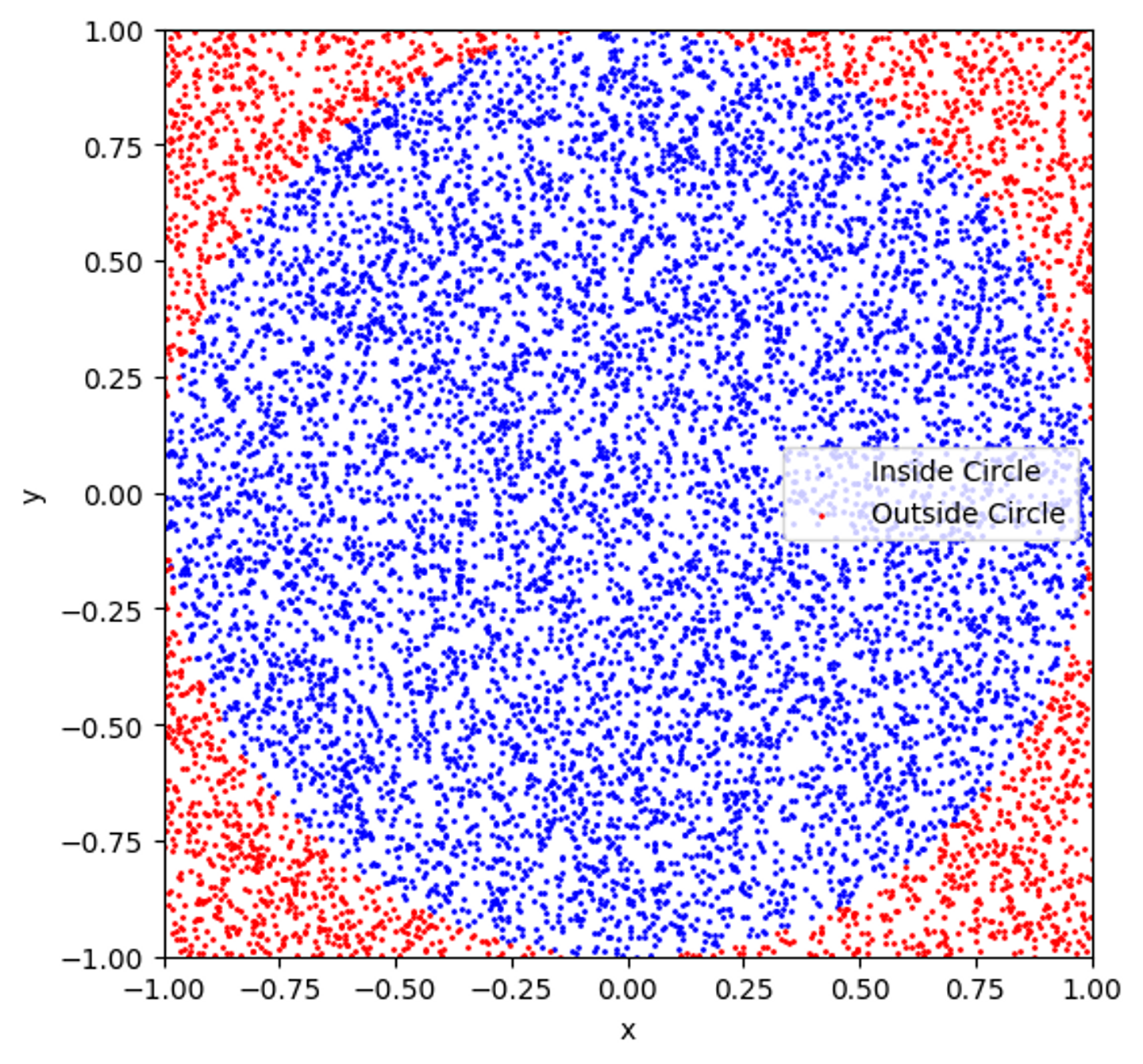
円の面積は同じ半径の正方形に円周率と1/4をかけることで求めることができます。
これを利用して、青い点の数を全体の点の数で割ることで実験的に円周率を求めることができます。
このように、膨大な数のシミュレーションを行い、その値の平均値を取ることで真の値を求めるのがモンテカルロ法です。
このモンテカルロ法を利用して今回は、選手の打率や長打力を設定し、膨大な試行回数のシミュレーションを行うことで得点の期待値を求めることを方針とします。
強打者を配置する打順によって、算出される得点の期待値に違いが出るかを調べていきましょう。
以下の手順で野球の試合をモデル化し、シミュレーションを実行します。
- 1番〜9番までの選手の打率と、打撃結果となるヒット種別の確率を設定する
- 野球の攻撃時を模したシミュレーションを9回分行う
- 事前に設定した試行回数分、試合のシミュレーションを行う
- 1試合に取った点数をそれぞれ記録し、すべての試合における平均値を取る
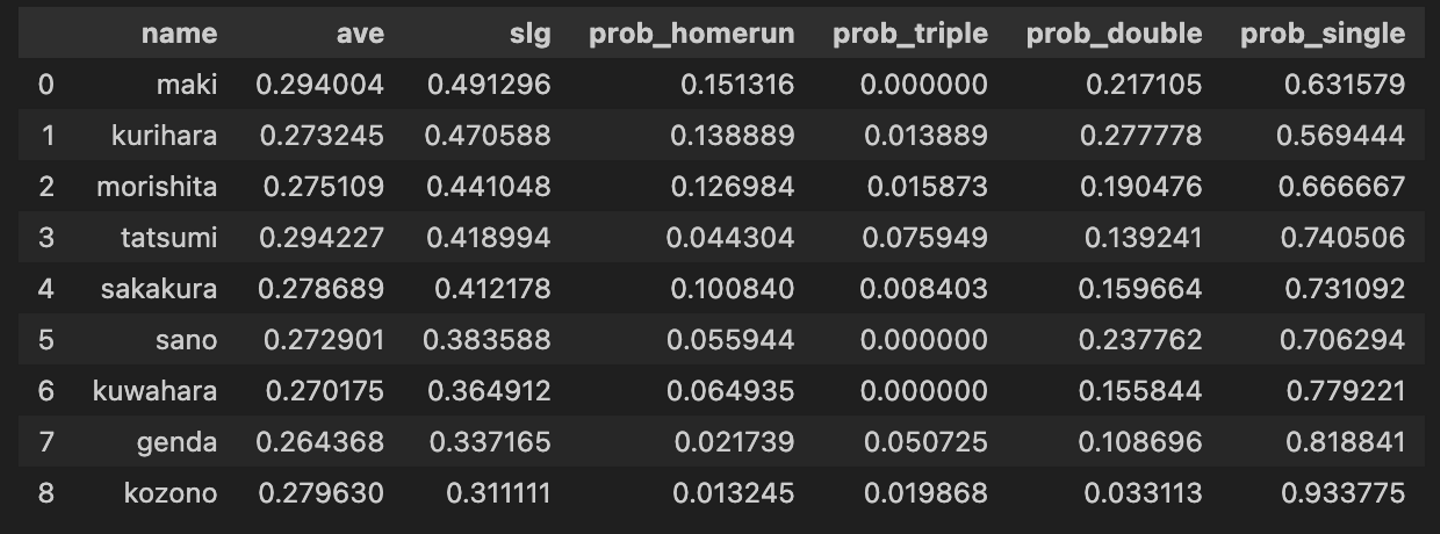
今回は、分かりやすい例として侍JAPANのメンバーのシーズン打撃成績を使って検証します。
NPB(日本野球機構)のホームページから、侍JAPANメンバーの昨年度の打撃成績を参照しました。
CSVファイルに以下のデータを入力します。(player.csv)
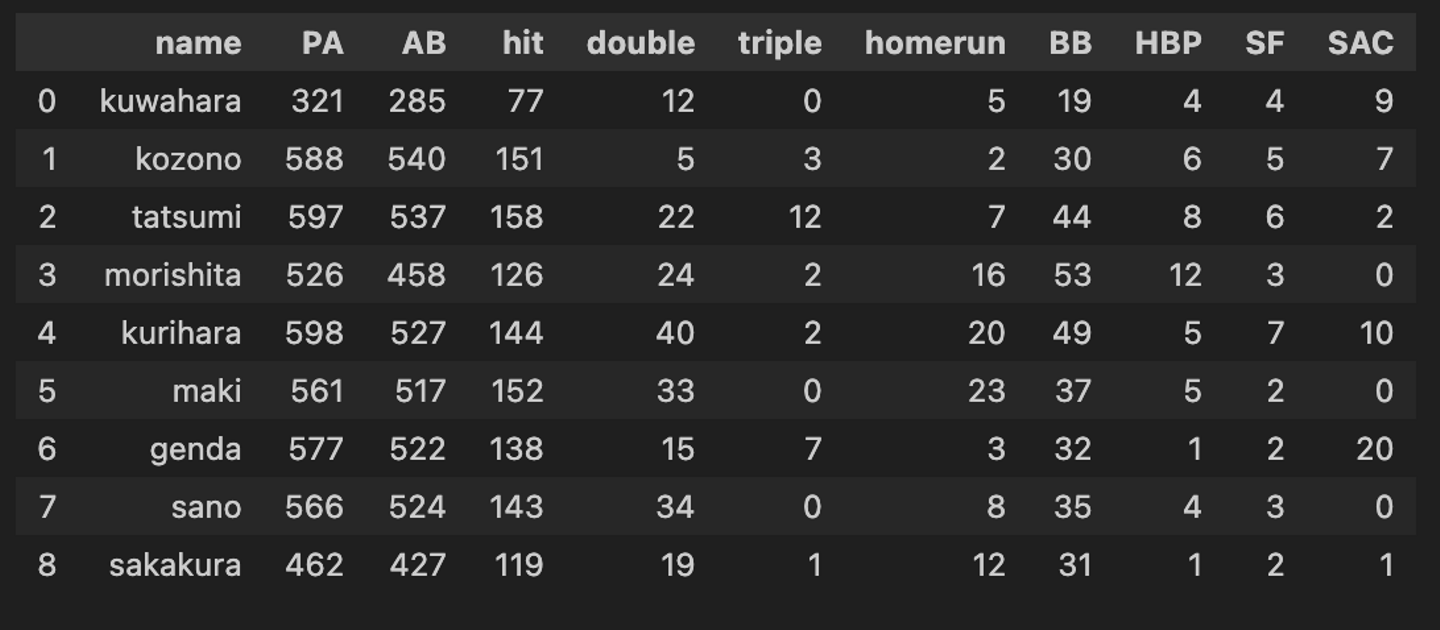
PAが打席数、ABが打数、hitが安打数です。
次はPythonで野球のシミュレーションを実装するコードを書いていきます。
検証~Pythonで実装してみる~

Pythonで今回のシミュレーションモデルを実装し、複数パターンにおける得点の期待値を検証していきます。
実装コード(Python)
まずはコードの全体像を見てみましょう。
import random
import pandas as pd
# シミュレーション回数
num_episodes = 1000000
# csvファイルを読み込んでdataframeを整理
df = pd.read_csv('player.csv')
df_player = df
df_player['ave'] = df_player['hit'] / df_player['AB']
df_player['prob_homerun'] = df_player['homerun']/df_player['hit']
df_player['prob_triple'] = df_player['triple']/df_player['hit']
df_player['prob_double'] = df_player['double']/df_player['hit']
df_player['prob_single'] = 1 - (df_player['prob_homerun'] + df_player['prob_triple'] + df_player['prob_double'])
df_player = df_player.iloc[:,11:]
# 打撃結果の内容を決定する関数
def determine_hit(player_row):
rand_value = random.random()
thresholds = [player_row[f'prob_{t}'] for t in ['single', 'double', 'triple', 'homerun']]
cumulative = 0
for hit_type, prob in zip(['single', 'double', 'triple', 'homerun'], thresholds):
cumulative += prob
if rand_value < cumulative:
return hit_type
return 'single'
# プレイヤーごとの打撃結果を決定する関数
def player_hit(player_row):
return determine_hit(player_row) if random.random() < player_row['ave'] else 'out'
# 塁の状態を管理する関数
def update_bases(bases, hit_type):
advance = {'single': 1, 'double': 2, 'triple': 3, 'homerun': 4}[hit_type]
score = 0
if advance == 4:
score = sum(bases) + 1
bases[:] = [0, 0, 0]
else:
for _ in range(advance):
score += bases.pop()
bases.insert(0, 0)
bases[advance - 1] = 1
return bases, score
# シミュレーション関数
def simulate_game(df_player, episodes=num_episodes):
results = []
PLAYER_CNT = 9
for _ in range(episodes):
score, outs, batter_idx, inning = 0, 0, 0, 1
bases = [0, 0, 0]
while inning <= 9:
outs = 0
bases = [0, 0, 0]
while outs < 3:
player_row = df_player.iloc[batter_idx % PLAYER_CNT]
hit_result = player_hit(player_row)
if hit_result == 'out':
outs += 1
else:
bases, run = update_bases(bases, hit_result)
score += run
batter_idx += 1
inning += 1
results.append(score)
if _ % (episodes/10) == 0:
print(f"{_/episodes*100}% complete")
return results
# 実行
scores = simulate_game(df_player)
print("Simulation Complete")部分ごとに、簡単に解説していきます。
まずは今回のコードに必要なライブラリをインポートし、シミュレーション回数を設定します。
シミュレーション回数が多ければ多いほど、実行時間は長くなりますが大数の法則に従って真の得点期待値に近づきます。
import random
import pandas as pd
# シミュレーション回数
num_episodes = 1000000先ほど用意したCSVファイルをpandasライブラリで読み込み、dataframeというテーブルの型として扱います。
この時、打率とヒットの種別が起こる確率を算出し、新しいテーブルの列として追加します。
# csvファイルを読み込んでdataframeを整理
df = pd.read_csv('player.csv')
df_player = df
df_player['ave'] = df_player['hit'] / df_player['AB']
df_player['prob_homerun'] = df_player['homerun']/df_player['hit']
df_player['prob_triple'] = df_player['triple']/df_player['hit']
df_player['prob_double'] = df_player['double']/df_player['hit']
df_player['prob_single'] = 1 - (df_player['prob_homerun'] + df_player['prob_triple'] + df_player['prob_double'])
df_player = df_player.iloc[:,11:]これで使うテーブルの準備が整ったので、シミュレーションを行うための関数を書いていきます。
最初の関数は、打撃の結果がヒットと決定された時、内容が一塁打、二塁打、三塁打、ホームランのいずれになるかを確率的に決定する関数です。
# 打撃結果の内容を決定する関数
def determine_hit(player_row):
rand_value = random.random()
thresholds = [player_row[f'prob_{t}'] for t in ['single', 'double', 'triple', 'homerun']]
cumulative = 0
for hit_type, prob in zip(['single', 'double', 'triple', 'homerun'], thresholds):
cumulative += prob
if rand_value < cumulative:
return hit_type
return 'single'安打かアウトかを決定する関数を書きます。
ランダムで0~1の値を取るrandomライブラリの関数を使い、値が打率を下回れば安打とします。
さらに先ほどのdetermine_hit関数によって安打の内容を決定し、出力します。
# プレイヤーごとの打撃結果を決定する関数
def player_hit(player_row):
return determine_hit(player_row) if random.random() < player_row['ave'] else 'out'次にランナーの状況を管理する関数を書きます。
野球は塁にいるランナーの数によって打撃の結果が変わります。
以下のような関数で打撃結果による塁の状況と点数を更新し、管理します。
# 塁の状態を管理する関数
def update_bases(bases, hit_type):
advance = {'single': 1, 'double': 2, 'triple': 3, 'homerun': 4}[hit_type]
score = 0
if advance == 4:
score = sum(bases) + 1
bases[:] = [0, 0, 0]
else:
for _ in range(advance):
score += bases.pop()
bases.insert(0, 0)
bases[advance - 1] = 1
return bases, score最後に試合内容を管理する、メインのシミュレーション関数を書いていきます。
1試合を9回、1回をアウトが3回重なるまでという繰り返し条件をつけ、バッターは順番に打順が回るようにします。
点数は変数scoreに格納し、試合ごとの点数を配列としてresultsに記録します。
# シミュレーション関数
def simulate_game(df_player, episodes=num_episodes):
results = []
PLAYER_CNT = 9
for _ in range(episodes):
# 試合の状況を初期化
score, outs, batter_idx, inning = 0, 0, 0, 1
bases = [0, 0, 0]
# 試合開始
while inning <= 9:
outs = 0
bases = [0, 0, 0]
while outs < 3:
player_row = df_player.iloc[batter_idx % PLAYER_CNT]
hit_result = player_hit(player_row)
if hit_result == 'out':
outs += 1
else:
bases, run = update_bases(bases, hit_result)
score += run
batter_idx += 1
inning += 1
# 試合の点数を記録
results.append(score)
# 実行の進捗状況を可視化
if _ % (episodes/10) == 0:
print(f"{_/episodes*100}% complete")
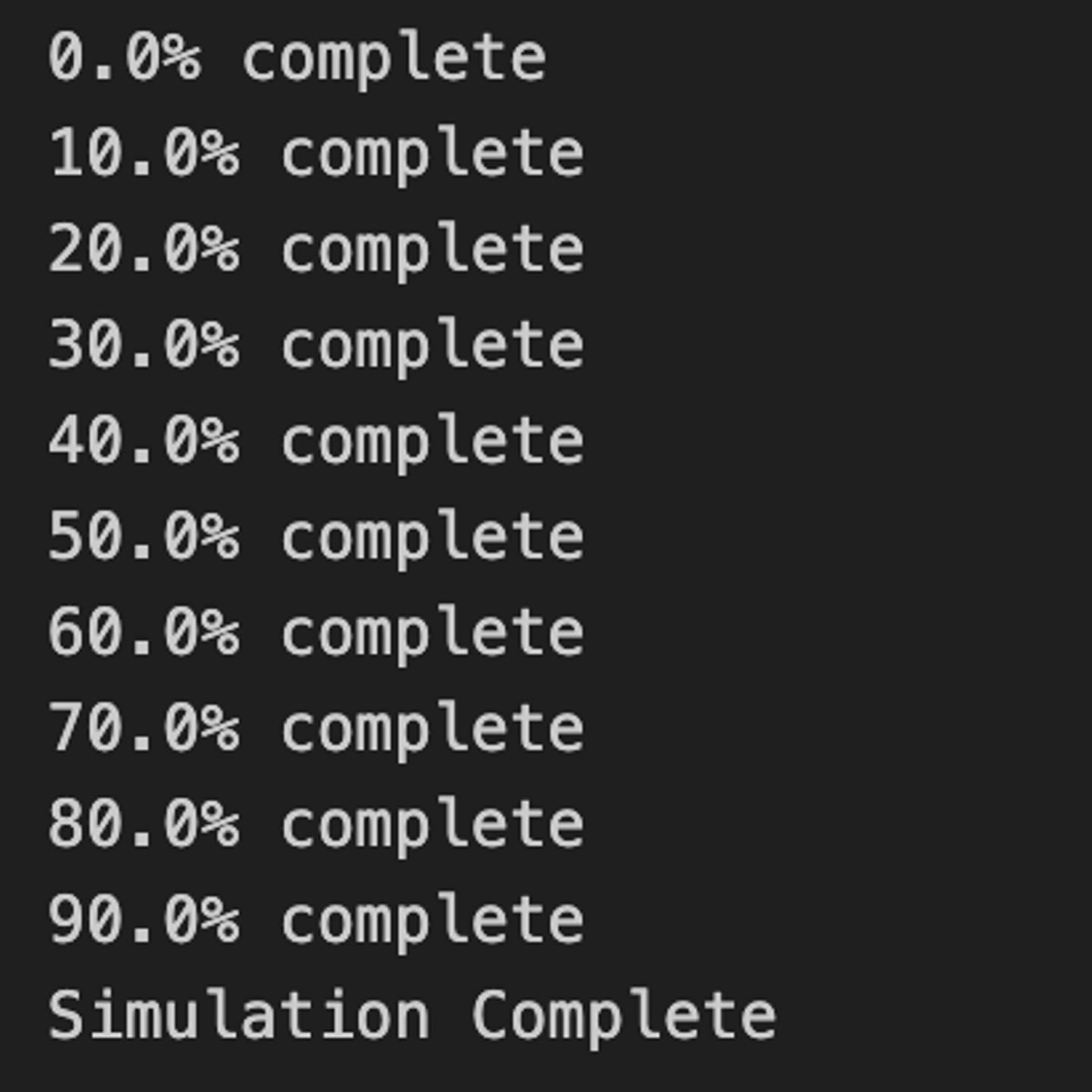
return results実行時間が長くなると予想されるため、以下のように記述して進捗状況をパーセンテージで可視化するのが良いでしょう。
# 実行の進捗状況を可視化
if _ % (episodes/10) == 0:
print(f"{_/episodes*100}% complete")これで準備は完了です!シミュレーション関数を実行しましょう。
# 実行
scores = simulate_game(df_player)
print("Simulation Complete")実行結果は、以下のように表示されるはずです。
1試合あたりの得点の平均を求め、期待値を算出してみましょう。
import statistics
statistics.mean(scores)
1,000,000回シミュレーションを実行した結果、1試合の平均は約2.586点となりました。
打順による値の違いを検証する前に、この値の信頼性を確認してみましょう。
大数の法則は「試行回数を増やすほど、試行によって計測された確率は真の確率の値に近づく」という法則でした。1,000,000回という値が十分かどうかを確かめます。
# エピソード数による、得点の平均値の変化をプロット
import matplotlib.pyplot as plt
episodes=len(scores)
scores_mean = scores[0]
list_scores_mean = [scores[0]]
for _ in range(episodes-1):
_ = _+1
scores_mean = (scores_mean*_ + scores[_])/(_+1)
list_scores_mean.append(scores_mean)
fig = plt.figure(figsize=(8, 5))
plt.plot(list_scores_mean)
plt.xlabel('Episodes')
plt.ylabel('Mean Score')
plt.ylim(2.56, 2.6)
plt.grid()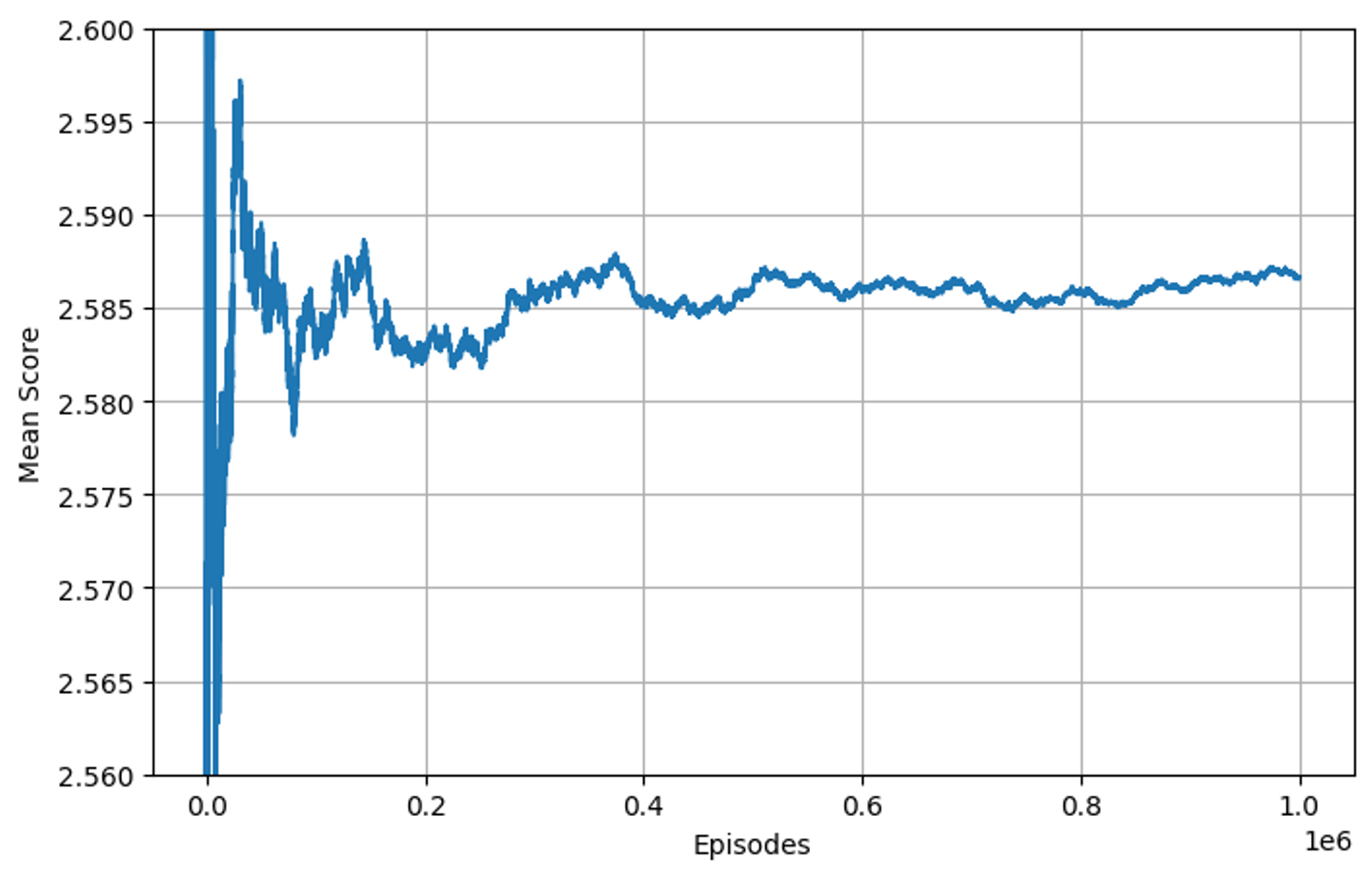
値はある程度収束しており、モデルの中の真の値として信頼性の高い計算結果であることが分かりました。
さて、いよいよ打順を入れ替えて期待値がどのくらい変わるかを検証していきましょう。
検証として、以下の3パターンで値がどのくらい変わるかを確かめてみます。
- クリーンナップ理論順
- 長打率順
- 打率順
①:クリーンナップ理論順
まずは、クリーンナップ理論に従って、長打力のある選手を4番→5番→3番に配置してみます。
長打力は長打率(SLG)と呼ばれる値を算出し、参考にします。
長打率(SLG) = (一塁打数 + 二塁打数×2 + 三塁打数×3 + 本塁打数×4) ÷ 打数この値を参考にし、SLGが高い選手から4番→5番→3番に配置しました。残りの打順は1番から打率順に配置しています。
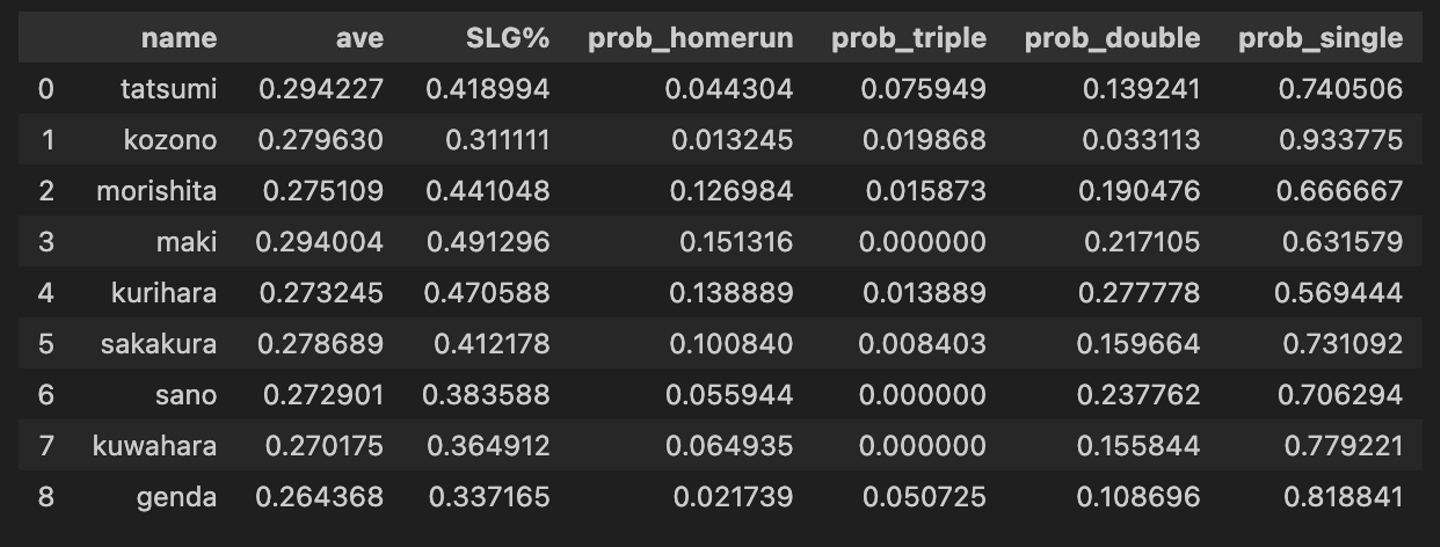
結果はこちらです。
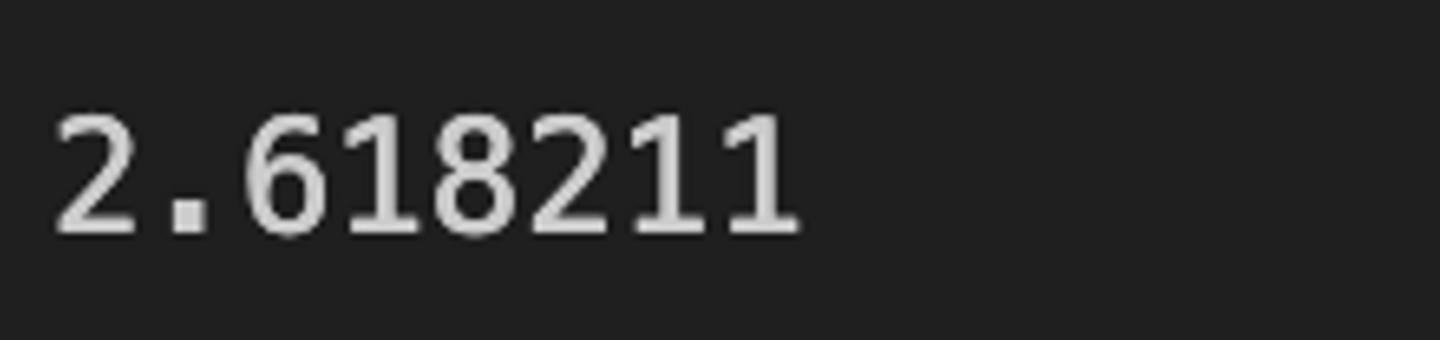
デフォルトの配置の場合よりも得点の期待値が上がりました。
先ほどと同様に、値が収束しているかどうかを確認してみましょう。
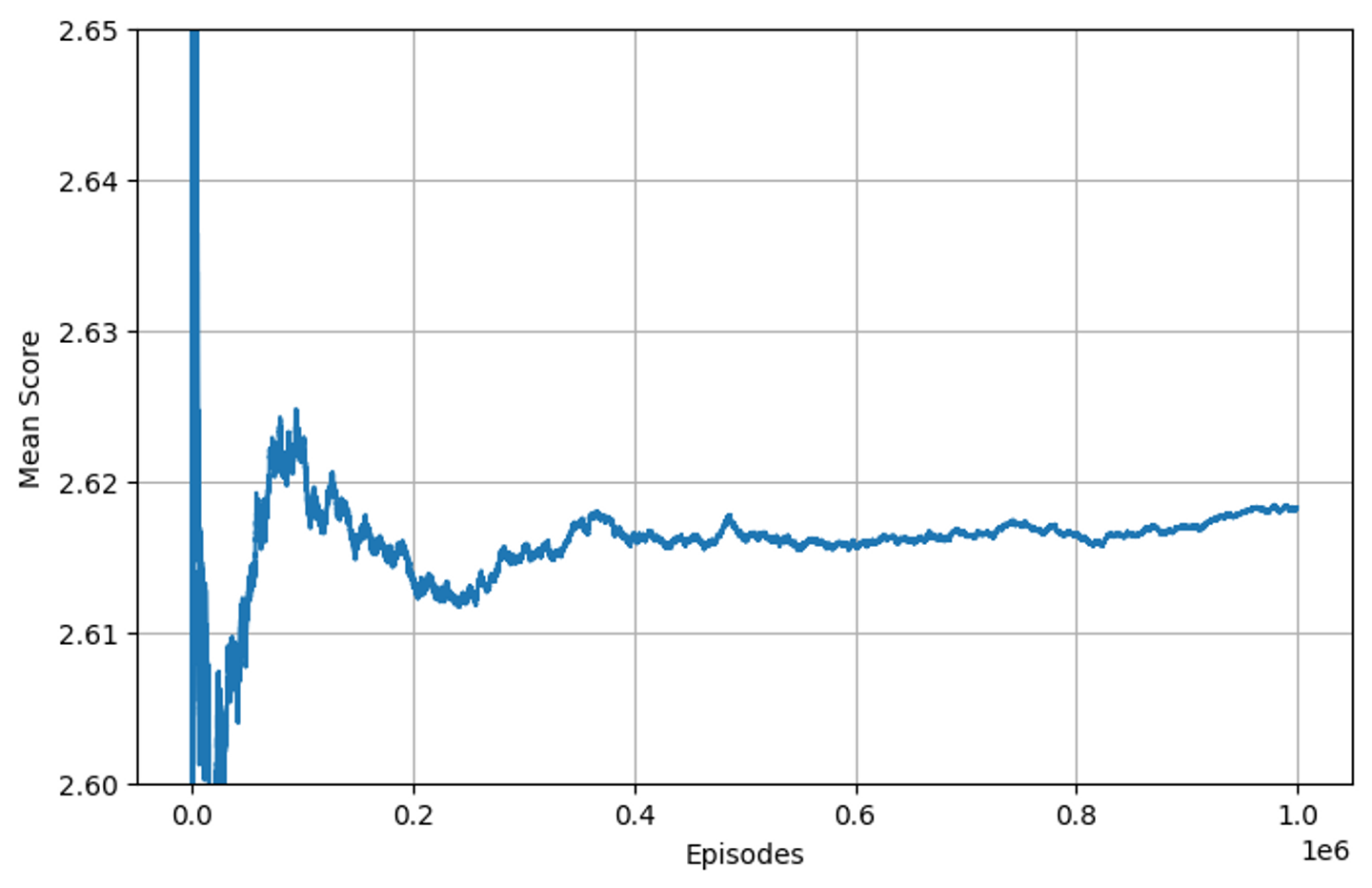
問題なさそうです。
得点ごとに、試合数をカウントした結果を見てみましょう。
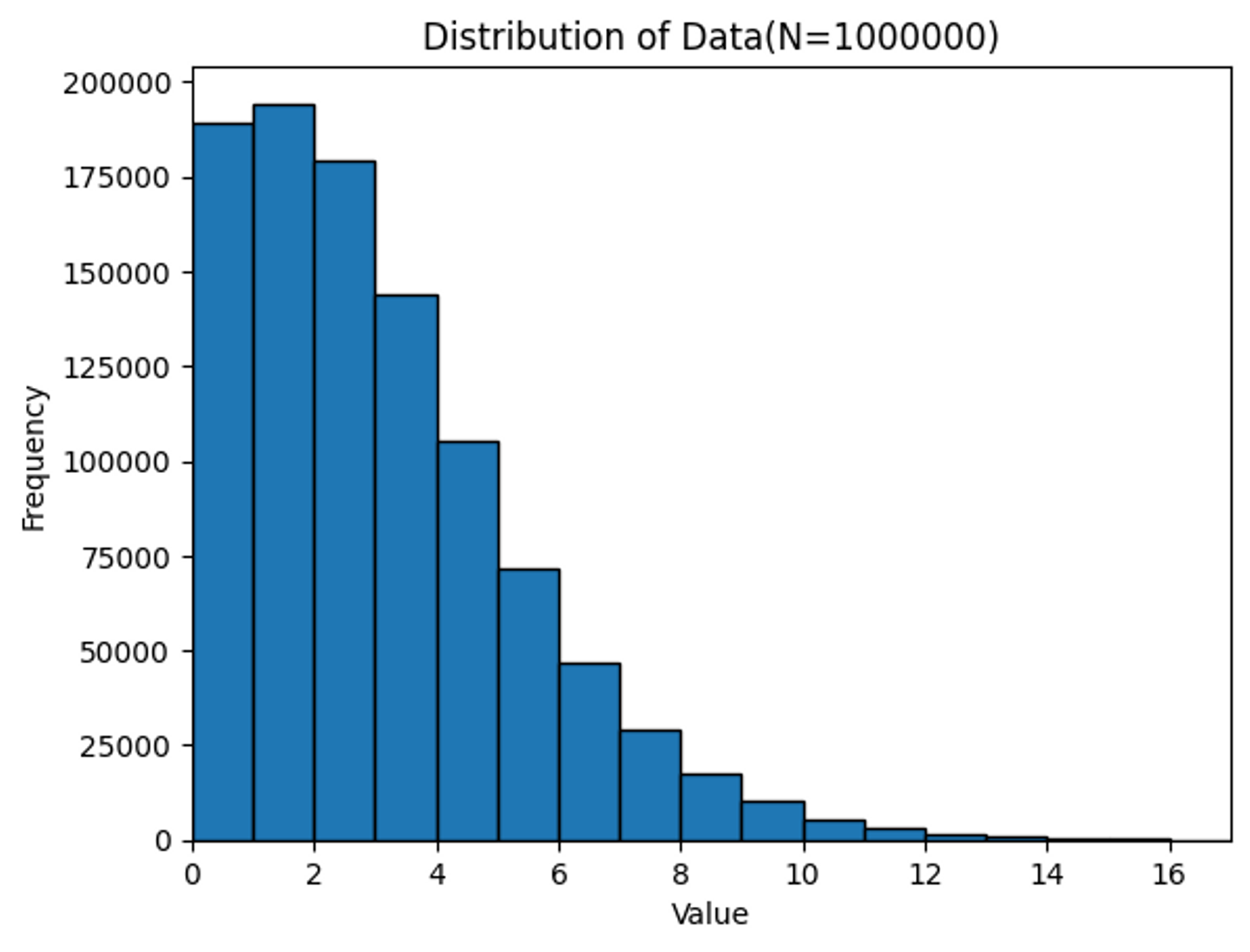
1点を取った回数が最も多く、次に0点、2点、3点と続いています。
②:長打率順
次に、長打率順に1番から配置した場合を見てみます。
早速実行し、結果を見てみます。

先ほどよりも得点の期待値が高くなりました。それぞれのグラフを確認してみましょう。
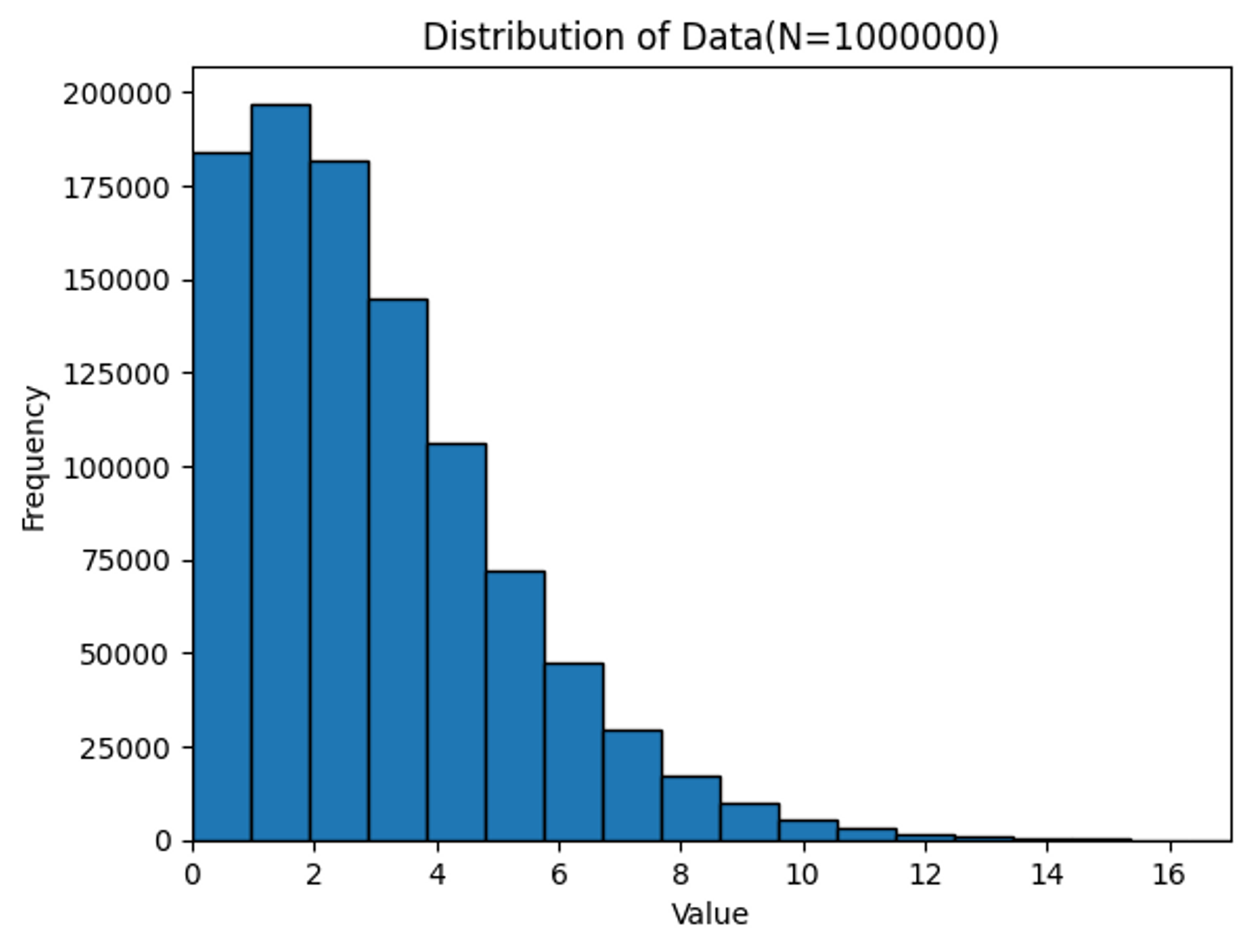
先ほどと比べ、0点である試合数が減り、1点の試合数が増えていることが分かります。
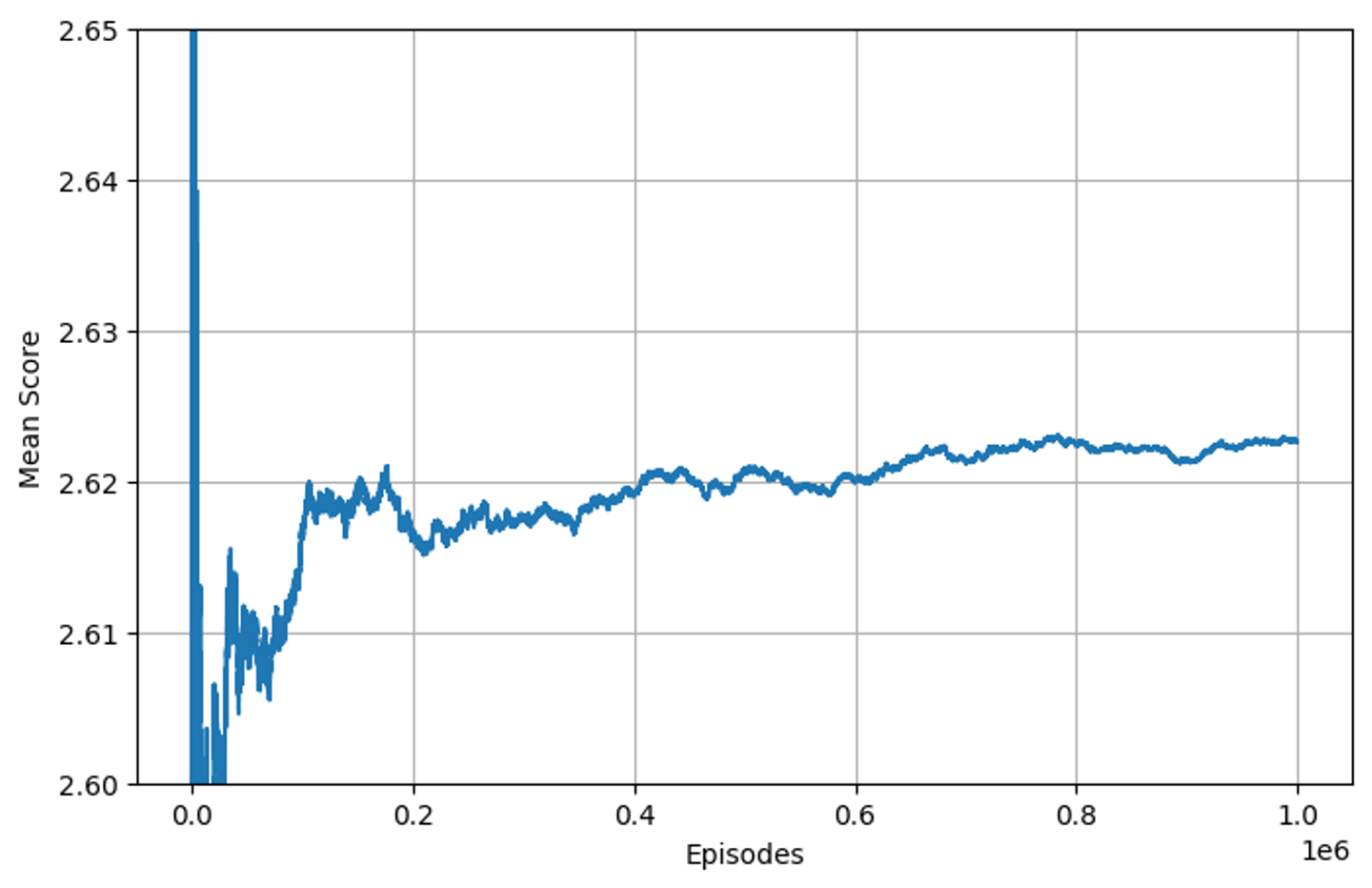
また、このグラフだけでは収束しているかどうかが怪しいので、試行回数5,000,000回でも実行してみましょう。

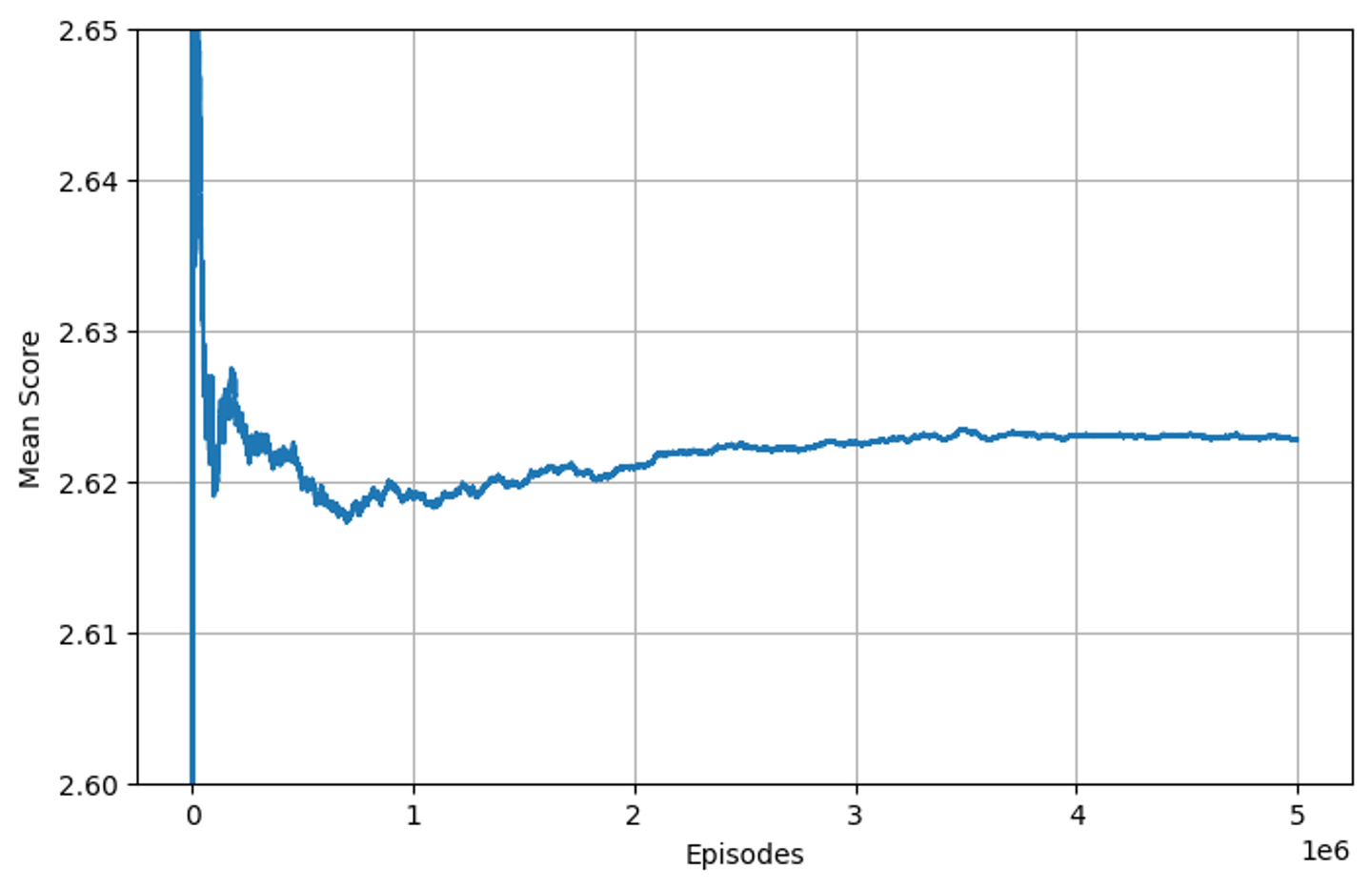
試行回数5,000,000回では値は綺麗に収束しました。
③:打率順
次に打率順に1番から配置した場合です。
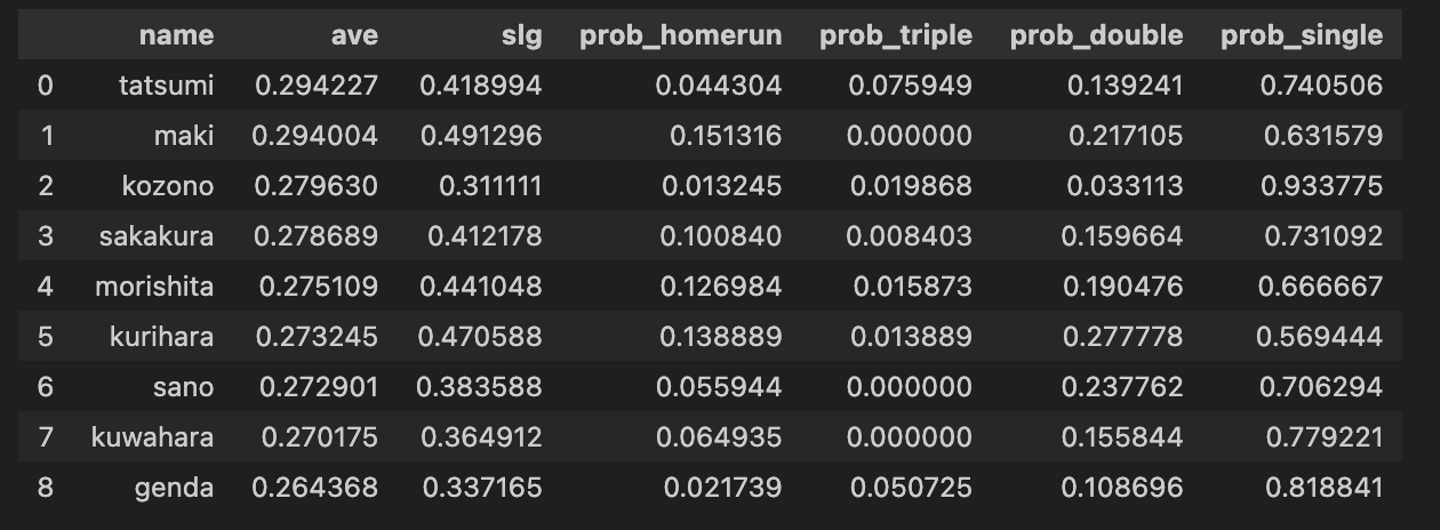
結果を見ていきます。
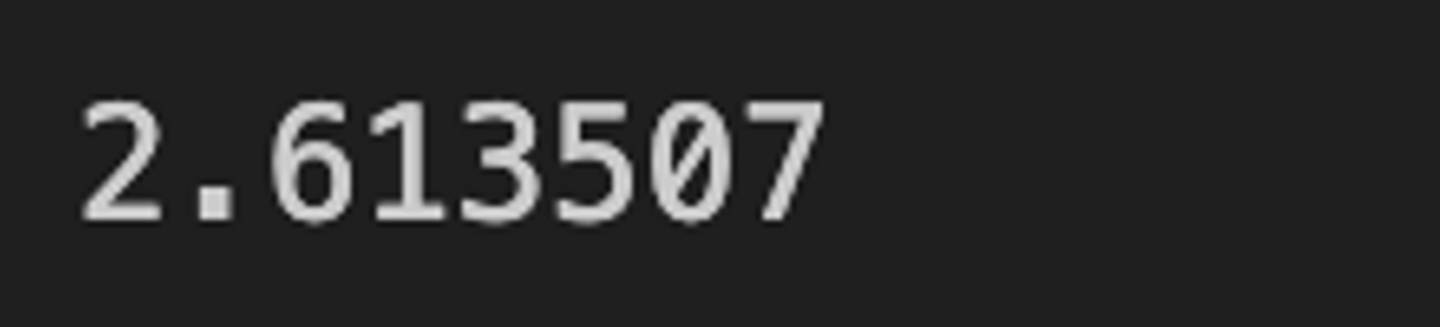
デフォルトの配置の場合よりは高くなっていますが、先ほどの2パターンよりも小さくなっています。
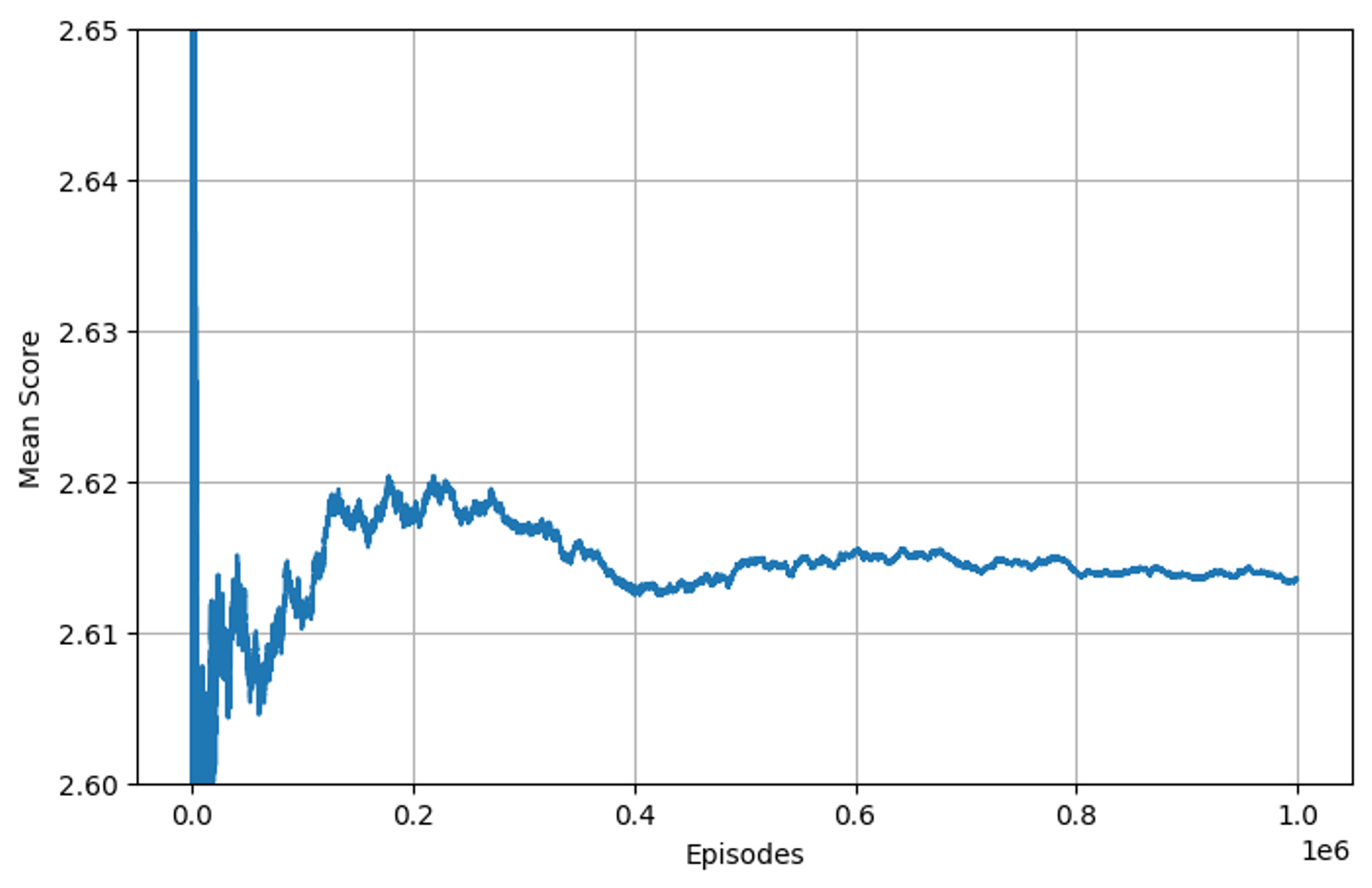
値の収束に関しては問題なさそうです。
ここまで3つのパターンを試しました。定量的な、点数ごとの試合数の分布をまとめてみましょう。
- パターン1:クリーンナップ理論
- パターン2:長打率順
- パターン3:打率順
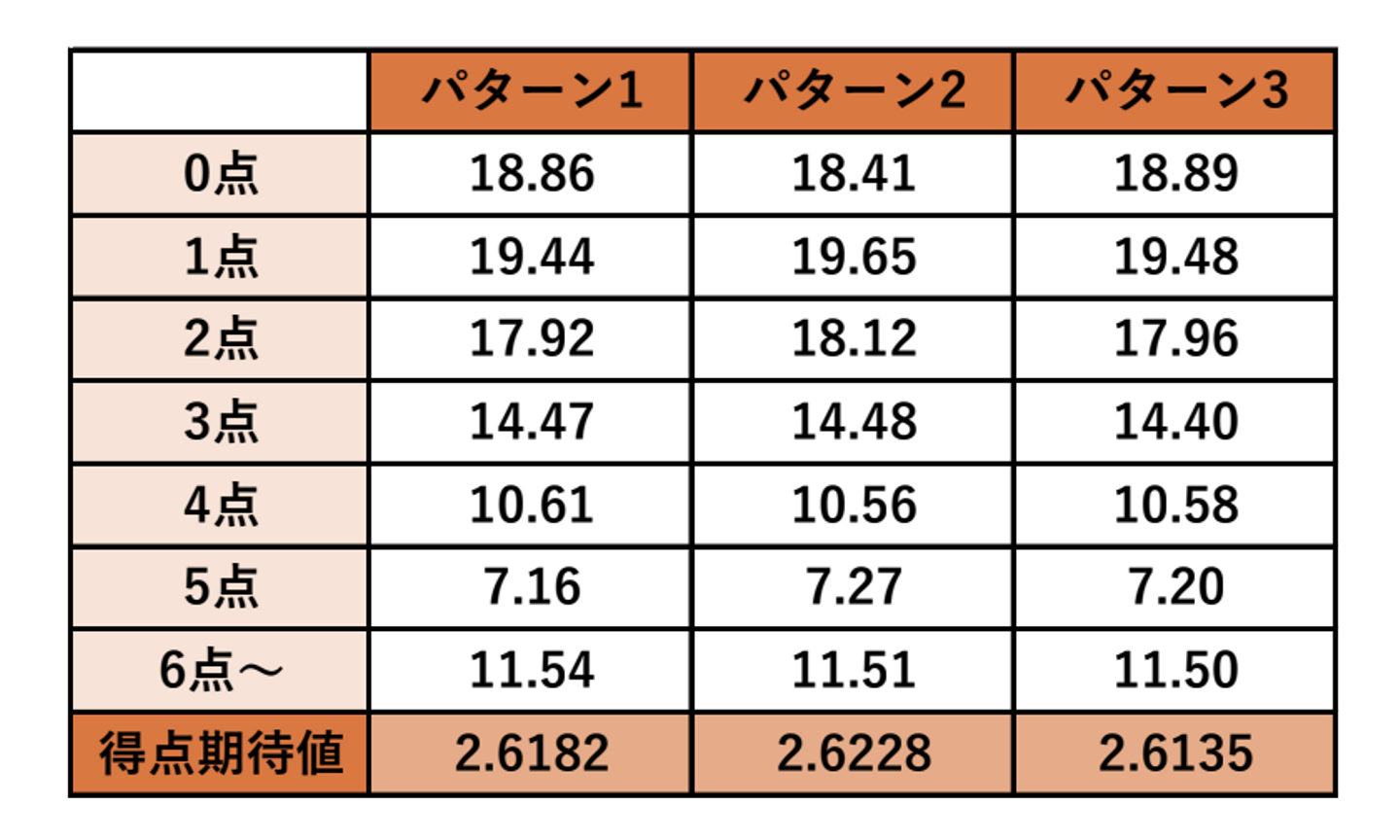
パターン2だけ、0点の割合が減り、1点と2点の試合の割合が増えていることが分かります。
これらの結果から、今回のモデルでは1番から長打率順に並べる打順が最も得点の期待値が高いという結果になりました。
他にも今回の結果から、
・今回検証した3パターンと、打順を適当に並べた時を比較すると明確な差が見られる
・3パターン同士の差はそこまで大きくはない
ということが言えます。
4番に強打者を置いた場合よりも、1番から順に強打者を置いた方が良いという直感に反した結果を得ることができました。
結果の信頼性について
今回はあくまで簡易的にモデル化した野球シミュレーションのため、前提条件を把握することも非常に重要です。
今回のシミュレーションモデルで再現できていない前提条件としては以下のようなものがあります。
- 三振と凡打は区別をしない(凡打でランナーは進まず、ダブルプレーも発生しない)
- バント、犠牲フライ、盗塁は発生しない
- 1塁打ならランナーは1つずつ進み、2塁打なら2つずつ進む。
もっと厳密に検証したい場合は、これらもより詳細に再現する必要があるでしょう。
また、今回は打撃のデータとして侍JAPANメンバーのシーズン成績を使いました。
つまり打率や長打率が高いメンバーのデータを使っているということであり、違うデータを使うとまた異なる結果が現れることでしょう。
実際にデータサイエンスを使って何か結論を得るときは、様々な前提や要因を考慮する必要があります。
ぜひ皆さんも、今回のコードを基に自分でモデルを改良し、検証してみてください!
おわりに
今回はスペースの都合上これ以上は書ききれませんでしたが、他にも色々な検証の方法があります。
強化学習を使えば、局面ごとにどのような戦略を使うと勝率が高くなるかが検証できます。
長打狙いか出塁狙いか、選手交代、バントのタイミングなど様々な判断を定量的に最適化することができるでしょう。
他にも深層学習を使えば勝敗の予測をすることができ、世の中にはそのような試みが多く行われています。
データサイエンスやAIを使って物事を予測・最適化することで、人間の感覚で為されてきた判断に、定量的な根拠を加えることができるのです。
このように、株式会社NucoではデータやAIの力で様々な問題解決を行なっています。
この記事を読んでデータサイエンスやAIが面白そうな世界だと感じたら、あなたも株式会社Nucoの仲間に加わりませんか?
興味を持っていただいたあなたからのエントリーをお待ちしています!

/assets/images/19438646/original/c5431c90-ce56-447b-b293-73302ad700ab?1729045386)

/assets/images/17033527/original/adf07eda-9151-44e3-bbfc-6d1193c0c364?1708089823)


/assets/images/17033527/original/adf07eda-9151-44e3-bbfc-6d1193c0c364?1708089823)